AI computer is self-learning: The end of Moore’s law?

A neuro-inspired analog computer that has the ability to train itself to become better at whatever tasks it performs has been developed by researchers. Experimental tests have shown that the new system, which is based on the artificial intelligence algorithm known as “reservoir computing,” not only performs better at solving difficult computing tasks than experimental reservoir computers that do not use the new algorithm, but it can also tackle tasks that are so challenging that they are considered beyond the reach of traditional reservoir computing.

The results highlight the potential advantages of self-learning hardware for performing complex tasks, and also support the possibility that self-learning systems—with their potential for high energy-efficiency and ultrafast speeds—may provide an extension to the anticipated end of Moore’s law. The researchers, Michiel Hermans, Piotr Antonik, Marc Haelterman, and Serge Massar at the Université Libre de Bruxelles in Brussels, Belgium, have published a paper on the self-learning hardware in a recent issue of Physical Review Letters.

“On the one hand, over the past decade there has been remarkable progress in artificial intelligence, such as spectacular advances in image recognition, and a computer beating the human Go world champion for the first time, and this progress is largely based on the use of error backpropagation,” Antonik told Phys.org. “On the other hand, there is growing interest, both in academia and industry (for example, by IBM and Hewlett Packard) in analog, brain-inspired computing as a possible route to circumvent the end of Moore’s law.

“Our work shows that the backpropagation algorithm can, under certain conditions, be implemented using the same hardware used for the analog computing, which could enhance the performance of these hardware systems.”

Developed over the past decade, reservoir computing is a neural algorithm that is inspired by the brain’s ability to process information. Early studies have shown that reservoir computing can solve complex computing tasks, such as speech and image recognition, and do so more efficiently than conventional algorithms. More recently, research has demonstrated that certain experimental implementations, in particular optical implementations, of reservoir computing can perform as well as digital ones.

In more recent years, scientists have shown that the performance of reservoir computing can be improved by combining it with another algorithm called backpropagation. The backpropagation algorithm is at the heart of the recent advances in artificial intelligence, such as the milestone earlier this year of a computer beating the human world champion at the game of Go.

The basic idea of backpropagation is that the system performs thousands of iterative calculations that reduce the error a little bit each time, bringing the computed value closer and closer to the optimal value. In the end, the repeated computations teach the system an improved way of computing a solution to a problem.

In 2015, researchers performed the first proof-of-concept experiment in which the backpropagation algorithm in conjunction with the reservoir computing paradigm was tested on a simple task.

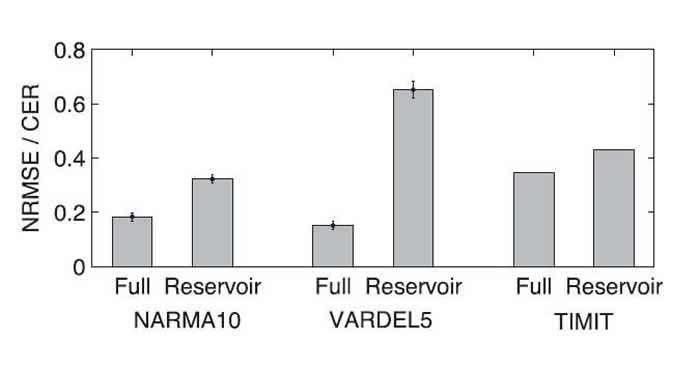
In the new paper, the researchers have demonstrated that the algorithm can perform three much more complicated tasks, outperforming reservoir computing systems that do not use backpropagation. The present system is based on a photonic setup (specifically, a delay-coupled electro-optical system) in which the information is coded as the intensity of light pulses propagating in an optical fiber. The key to the demonstration is to physically implement both the reservoir computer and the backpropagation algorithm on the same photonic setup.

The three tasks performed were a speech recognition task (TIMIT), an academic task often used to test reservoir computers (NARMA10), and a complex nonlinear task (VARDEL5) that is considered beyond the reach of traditional reservoir computing. The fact that the new system can tackle this third task suggests that the new approach to self-training has potential for expanding the computing territory of neuromorphic systems.

“We are trying to broaden as much as possible the range of problems to which experimental reservoir computing can be applied,” Antonik said. “We are, for instance, writing up a manuscript in which we show that it can be used to generate periodic patterns and emulate chaotic systems.”

While the demonstration shows that the new approach is robust against various experimental imperfections, the current set-up is limited by the speed of some of the data processing and data transfer, which the researchers expect can be improved in future work.

“We aim to increase the speed of our experiments,” Antonik said. “The present experiment was implemented using a rather slow system, in which the neurons (internal variables) were processed one after the other. We are currently testing photonic systems in which the internal variables are all processed simultaneously—we call this a parallel architecture. This can provide several orders of magnitude of speed-up. Further in the future, we may revisit physical error backpropagation, but in these faster, parallel, systems.”

More information: Phys.org